Teorema de Bayes e a inferência bayesiana
Teorema de Bayes e a inferência bayesiana
Teorema de Bayes, na teoria da probabilidade e estatística, trata-se de um meio para revisar as previsões à luz de evidências relevantes. Esse teorema é também conhecido como probabilidade condicional ou probabilidade inversa.
O teorema foi descoberto entre os papéis do ministro/pastor e matemático presbiteriano inglês Thomas Bayes (1701-1761) e publicado postumamente em 1763. Por isso esse teorema de Bayes recebe este nome, Teorema de Bayes.
Ele foi o primeiro a fornecer uma equação que permitiria que novas evidências atualizassem a probabilidade de um evento a partir do conhecimento a priori (ou a crença inicial na ocorrência de um evento).
O Teorema de Bayes é uma fórmula matemática simples usada para calcular probabilidades condicionais. Ele figura com destaque nas abordagens subjetivistas ou bayesianas da epistemologia, estatística e lógica indutiva.
Os subjetivistas, que sustentam que a crença racional é governada pelas leis da probabilidade, apoiam-se fortemente nas probabilidades condicionais em suas teorias de evidências e em seus modelos de aprendizagem empírica.
O Teorema de Bayes é central para essas empresas porque simplifica o cálculo de probabilidades condicionais e porque esclarece características significativas da posição subjetivista.
Na verdade, o insight central do Teorema – que uma hipótese é confirmada por qualquer corpo de dados que sua verdade torne provável – é a pedra angular de toda metodologia subjetivista.
Inferência bayesiana
Uma das muitas aplicações do teorema de Bayes é a inferência bayesiana, uma abordagem particular da inferência estatística. Quando aplicado, as probabilidades envolvidas no teorema de Bayes podem ter diferentes interpretações de probabilidade.
Com a interpretação bayesiana de probabilidade, o teorema expressa como a probabilidade de um evento (ou o grau de crença na ocorrência de um evento) deve ser alterada após considerar evidências sobre a ocorrência deste evento
Portanto temos relacionado ao teorema, a inferência bayesiana, ou bayesianismo, baseada na atribuição de alguma distribuição a priori de um parâmetro sob investigação. O teorema mostra como alterar as probabilidades *a priori tendo em vista novas evidências para obter probabilidades *a posteriori.
*a priori: quer dizer que a distribuição de probabilidade dos parâmetros é atribuída antes de se observar os elementos amostrais.
*a posteriori: quer dizer que a distribuição de probabilidade dos parâmetros é atualizada após observar os elementos amostrais.
O teorema de Bayes é expressa matematicamente na forma da seguinte equação:
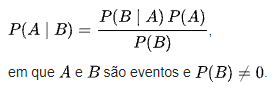
- P (A) e P (B) são as probabilidades a priori de A e B.
- P (A \ B) é a probabilidade a posteriori (probabilidade condicionada) de A condicional a B.
- P (B \ A) é a probabilidade a posteriori (probabilidade condicionada) de B condicional a A.
O teorema de Bayes não é uma solução milagrosa quando olhamos para a sua fórmula simples como vemos. O mais importante que essa fórmula são as “entradas”, ou seja, o quão exatas são as informações.
A chave de um resultado ótimo parte do princípio de que as estimativas sobre probabilidades prévias sejam de qualidade, para que esse teorema nos entregue resultados mais confiáveis possível.
Aplicação do Teorema de Bayes
O teorema de Bayes relaciona informações, com a probabilidade de ocorrência, para gerar uma nova probabilidade. Isso acontece quando os fatos acontecem de maneira relacionada ou são dependentes. Seus resultados não podem ser considerados “definitivos” pois tais probabilidades podem e devem ser revistas à medida que são observados novos fatos. Isso pode alterar a probabilidade de cada um dos acontecimentos envolvidos (SILVER, 2013).
O teorema de Bayes utiliza incertezas, entretanto é alimentado por meio de probabilidades que podem ser estimas ou sugeridas. Baseado nesse princípio fica entendido que esse teorema trabalha primeiramente com informações prévias.
Dessa forma, ao obter novas informações aplica-se o teorema e alcançam-se as probabilidades posteriores. O teorema de Bayes utiliza dois tipos de inferências estatísticas:
Inferência intuitiva: é adquirida através do conhecimento prévio em relação a situações passadas, desta maneira pode-se fazer uma conjectura sobre a situação e formular uma possível probabilidade.
Inferência experimental: se obtém através da experimentação, a partir dos dados são feitos procedimentos estatísticos com os quais se calcula a probabilidade, à medida que novos dados são coletados, são refeitos os cálculos estatísticos e calculadas as novas probabilidades.
A abordagem Bayesiana tem sido aplicada na medicina, em diversas análises e cenários, avaliações de risco no meio empresarial e uso na tecnologia (ciência de dados). Por isso, esse teorema é aplicado na construção de diversos algoritmos, que por sua vez favorecem a darem uma resposta mais precisa.
Conclusão
O Teorema de Bayes acredita-se ser o mais importante teorema no campo da estatística matemática e da teoria da probabilidade. A crescente onda de inteligência artificial – IA e do Aprendizado de máquina aumenta a capacidade das máquinas e equipamentos.
De modo que a abordagem Bayesiana faz com que a proposta de Bayes seja cada vez mais útil. Portanto trata-se de um recurso excelente para ser usado em diversas ferramentas de análises. Com isso poder avaliar diversos tipos de eventos para entender as probabilidades de certas ocorrências.
Isso com certeza se torna um passo à frente para eliminar ou minimizar muitos problemas. Pode trazer algumas sugestões de ações e agir de forma assertiva para evitar essas ocorrências indesejáveis. Como mostra de sua grande utilidade no meio industrial temos um estudo da universidade de Osaka sobre vida útil dos rolamentos.
Cientistas do Instituto de Pesquisa Científica e Industrial e dos Laboratórios NTN Next Generation Research Alliance da Universidade de Osaka desenvolveram esse estudo.
Trata-se de um estudo sobre a rede neural artificial – RNA, método de aprendizado de máquina que combina redes neurais convolucionais e modelagem hierárquica bayesiana para prever com precisão a vida útil restante dos rolamentos. Este trabalho pode levar a novos métodos de monitoramento industrial (preditiva) que ajudam a gerenciar os programas de manutenção e maximizar a eficiência e segurança sob a evolução de falhas.
Fonte:
https://pt.wikipedia.org/wiki/Teorema_de_Bayes