Curva da banheira – parte II
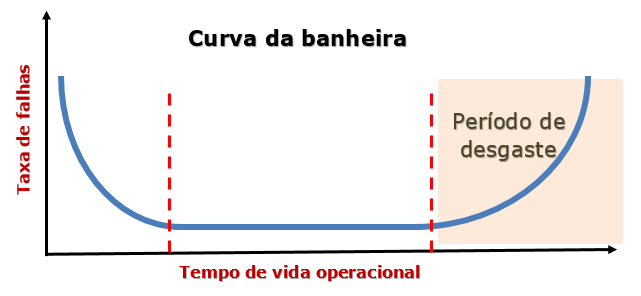
Curva da banheira – parte II
Dando continuidade a matéria sobre a “Curva da banheira”, nesta segunda parte vamos ver sobre o período da taxa de falha e sobre o período de desgaste.
-
O período de taxa de falha constante
4.1 Explicação geral do período de vida útil
O período de mortalidade infantil é seguido por um período de falha quase constante conhecido como “vida útil”. Nesta região, as falhas ocorrem por pura casualidade.
Adicionalmente, como a taxa de falha é constante, esta é a única região, em que a distribuição exponencial pode ser válida e, portanto, o tempo entre as falhas é distribuída exponencialmente.
4.2 – Identificar e quantificar falhas na vida útil
Juran (1988) acha que o fracasso desse período resulta da limitação inerente de projeto e acidentes causados pelo uso ou manutenção inadequada. Por outro lado, como a taxa de falhas durante este período é constante, a taxa de falha segue distribuição exponencial (ou distribuição de Weibull com o parâmetro de forma de b=1).
O mecanismo da distribuição exponencial, como Juran (1988) apontou, é que de falhas aleatórias que são independentes da vida acumulada e, consequentemente, são individualmente imprevisíveis.
Esse mecanismo é importante para a confiabilidade do sistema de cálculo, que é frequentemente assumido que a “confiabilidade do sistema é o produto da confiabilidade individual das inúmeras partes dentro do sistema” (Juran, 1988). Essa é a chamada “regra do produto”:
Como a “regra do produto” também pressupõe:
- Que as falhas de qualquer parte causam falha do sistema, e;
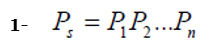
- A confiabilidade das partes são, independentes umas das outras. Então quando cada parte segue distribuição exponencial, então:
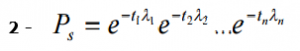
Além disso, se “t” é o mesmo para cada parte:
![]()
Portanto, quando a taxa de falha é constante, a confiabilidade do sistema pode ser prevista pela adição da taxa de falha da peça.
Embora a suposição nem sempre seja válida e a suposição de distribuição exponencial deve ser apoiada pela coleta de dados de falhas, ainda por causa da simplicidade da função de densidade exponencial, tem sido amplamente utilizado no trabalho de confiabilidade.
Mas Jensen (1990) argumenta que no padrão de banheira, a taxa de falha constante (ou quase constante) é encontrada estritamente em testes de vida. Durante estes testes a flutuação aleatória não ocorre. Juran (1988) também admite que a suposição de taxa de falha constante é justamente questionada.
Mas a experiência sugere que esta suposição é muitas vezes necessária em se fazer (Juran, 1988). Além disso, ele acredita que tomar ações de projeto para produzir uma taxa de falha constante é mais fundamental do que argumentar a validação da suposição.
4.3 – Eliminar falhas na ‘vida útil’
De acordo com a visão de Juran (1988), um bom controle sobre os procedimentos de operação e manutenção pode ser aplicado para eliminar as falhas durante o período de vida útil, causadas pela má manutenção ou uso inadequado. No entanto, a redução básica da taxa de insucesso requer um redesenho básico.
Diferentemente, Ebeling (1997) sugere usar redundância para reduzir falhas durante a “vida útil”. Ascher (1984) argumenta que esses tipos de contradições podem resultar da ignorância e incompreensão da existência de “duas curvas de banheira”, uma é “um modelo para uma população de peças e componentes e a outra curva de banheira com uma interpretação diferente é um modelo para um sistema’.
Além disso, é digno de atenção que a diminuição da taxa de falhas durante o período de vida útil (ou aumento no MTBF para o componente reparável) não resulta em um aumento proporcional na confiabilidade (a probabilidade de sobrevivência).
Por exemplo, na equação R = e –l, se t = 1h. Um aumento de cinco vezes em MTBF de 20 para 100h só pode produzir 4% de aumento na confiabilidade.
Mas ao aumentar o MTBF de 5 para 10h, o aumento de 8% pode ser obtido na confiabilidade. A compreensão deste caráter exponencial é importante, pois a taxa de falha ou MTBF são sempre utilizados como critérios para a tomada de decisão, o que afetará a confiabilidade, enquanto “A probabilidade de sobrevivência por um tempo especificado “t” pode ser o índice mais importante para o cliente” (Juran, 1988).
4.4. Algumas curvas de banheira específicas
Diferentes tipos de componentes podem exibir variações significativas nesta forma básica da banheira.
Algumas das diferenças representam o período de vida útil. Billington (1992) acredita que dois exemplos específicos cobrem os dois casos extremos, eles são: componente eletrônico e componente mecânico.
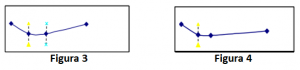
Comparando-se com componentes mecânicos, os componentes eletrônicos (veja a Figura 2) geralmente são associados a uma vida útil longa relativa, enquanto que para componentes mecânicos (veja a Figura 3), este período é muito breve.
Além disso, Slack (2001) também aponta que, para as falhas de operação que dependem mais de recursos humanos do que de tecnologia, a vida útil da curva da banheira não é evidente e o período de falha inicial pode ser seguido por um longo período de falha crescente (veja figura 4).
Além disso, algumas pesquisas recentes na indústria eletrônica identificaram outro padrão de falha: falha latente.
As causas de falha latente são as falhas não detectadas, que “não podem ser facilmente descartadas por inspeção ou testes funcionais até que seja transferida para um defeito de patente pelo estresse ambiental aplicado ao longo do tempo” (Yan, 1997).
A característica da falha latente é quando as tensões, tanto internas quanto externas, excedem a força do sistema; haverá um salto na curva de taxa de falha devido à ocorrência de falha latente. (Veja a Figura 5)

Além disso, Yan (1997) também argumenta que na curva da banheira convencional, o tempo de falha é assumido como contínuo entre zero e infinito. No entanto, na prática, a vida útil da maioria dos sistemas eletrônicos é finita.
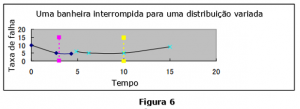
O fator de obsolescência tecnológica deve ser considerado. Portanto, a combinação de obsolescência técnica e defeitos latentes pode ser “modelada como uma distribuição de mistura interrompida” (Yan, 1997), (Veja a Figura 6).
No entanto, como Yan (1997) apontou, embora a forma real da curva da banheira possa ser variada, a forma geral permanece a mesma “.
-
O período de desgaste
5.1 Explicação geral do período de desgaste
O período de desgaste é caracterizado por uma rápida taxa de falha crescente com o tempo. Do ponto de vista de Billington (1992), este período é mais evidente do que os outros dois períodos como nesta região, a função de densidade de falhas aumentará em primeiro lugar, e depois diminuirá para zero para a obsolescência dos componentes.
5.2. Identificar e quantificar o período de desgaste das falhas
No período de desgaste, a função de densidade de falha pode ser frequentemente representada ou aproximada pela distribuição normal. A distribuição gama e Weibull também pode ser usada para quantificar falhas durante o período de desgaste.
A razão é que essas distribuições possuem parâmetros de modelagem, “a variação de que pode criar uma forma característica significativamente diferente” (Billington, 1992).
Além disso, Billington (1992) aponta que, se a região de desgaste estiver distribuída de forma normal, “o tempo em que entra na região de desgaste depende do desvio padrão da distribuição”.
No entanto, Billington (1992) também lembra que a previsão de confiabilidade baseada na taxa de falha da “vida útil” é inválida e extremamente otimista para ser usado com o período de desgaste. Por outro lado, embora a taxa de falha da “vida útil” seja analítica simples e o “período de vida útil pode ser prolongado por manutenção e substituição preventiva cuidadosa e regular”. Na prática, o componente pode falhar muito antes do MTBF ou MTTF ser alcançado Devido ao desgaste.
5.3. Elimine falhas no período de desgaste
Juran (1988) sugere que as falhas durante o período de desgaste são devidas à vida útil. Na sua opinião, para reduzir as falhas é necessário levar a efeito a substituição preventiva dos componentes no final da sua vida útil. Ebeling (1997) concorda com isso e adiciona manutenção preventiva como outro método para reduzir falhas durante o período de desgaste.
Cater (1986) observa ainda que, para o sistema mecânico com manutenção ideal (isto é, todos os componentes com falha serão substituídos por componentes idênticos sem alterar o sistema), a taxa de falha do sistema pode permanecer no estado estacionário e, em seguida, a seção de desgaste da curva da banheira poderia ser eliminada.
Mas Cater (1986) também admite que, na prática, essa “manutenção ideal” não é praticável. Pelo contrário, o desgaste efetivo pode impedir o reparo desnecessário ou não econômico de equipamentos mecânicos.
5.4 Argumentos sobre os períodos de desgaste
Embora o período de desgaste da curva da banheira seja amplamente aceito, alguns pesquisadores ainda questionam a forma e a existência da seção de desgaste da curva da banheira.
George (2000) argumenta que as estimativas não paramétricas da função de taxa de falha podem revelar alguma coisa inesperada, que é “a curva da banheira nem sempre contém água”, (Figura 7).
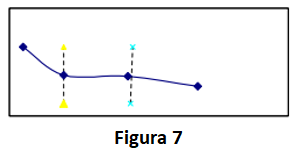
Ele lembra a atenção e aponta que a revisão ou reforma antecipada (preventiva), que significa “menos horas de operação por unidade de tempo do calendário” (George, 2000) também pode causar a diminuição da taxa de falha. A “banheira” não contém água quando essa revisão ou reforma ocorreu antes do desgaste.
Da mesma forma, Ascher (1984) também argumenta que, embora a teoria da curva da banheira represente a visão de muitos engenheiros de confiabilidade e seja um modo melhor para algum sistema, a curva da banheira do sistema reparável contradiz os teoremas de limitação.
O teorema de limitação, que está ilustrado na Figura 8, indica que o sistema irá se estabelecer com um valor constante na região de vida longa, exatamente onde a curva da banheira prevê que a taxa de falhas aumentará acentuadamente.
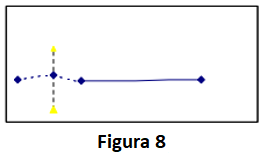
Além disso, como Ascher (1984) apontou a reconciliação entre a curva da banheira e os teoremas de limite, uma curva mostrará um período de desgaste discreto.
Além disso, Tsang (1995) declara que um extenso estudo na indústria de aviação prova que a curva da banheira não é um modo universal que se aplica a todos os itens, e “tanto quanto 89% de todos os itens de equipamentos da companhia aérea não são visíveis na região de desgaste ao longo de sua vida útil “(Tsang, 1995).
-
Conclusão
A curva da banheira é um modelo comum para descrever a taxa de falha de uma população e foi amplamente aceita como uma ferramenta de engenharia. No entanto, como discutido acima em algumas situações, a teoria típica da banheira não é tão convincente.
Portanto, é realmente necessário combinar os métodos, que são usados para identificar e eliminar as falhas juntas e implementá-las como um programa coerente de qualidade e confiabilidade, visando a função real necessária, condições especificadas e período específico, associado à consideração de custos, requisitos do cliente, projeto, negócios e práticas de fabricação também.
Fonte: CATSI – China Association for Technical Supervision Information